Hacker Math

Numbers are important in our world in fact number systems are the base of reason for alot of things around us. What is your age? When is your birthday? What's your phone number? All of the answers to those questions are related to numbers. Even when you are reading a book or a blog post like this you are tracking words, pages and sentences all in a numerical way. Number systems appear in many ways throughout our lives, the one you are most familiar with is probably Base-10 which is the most common 1..10,11,12...100. This system. also called Decimal, most likely derived from the amount of fingers on an average human, 10; who hasn't counted something with their fingers. As for computers at the lowest level uses Base-2, which is usually referred to as binary, the system based out of 1's and 0's. So you are probably wondering if there are any other base systems, the answer is yes. You can make a number system with any base you want but these are the most common ones: Base-2 (Binary) Base-8 (Decimal) * Base-16 (Hexadecimal)

So what are bases you ask? Well that is a little beyond what I want to get into during this article but basically a Base number is the number of units counted before the unit is carried over as a multiple. For example in Base-10 you will never see a number higher than 9 in a Base-10 number as the last digit. So using that concept in Base-2 you will never a value higher than 1 as the last digit. So to represent a number like 3 you need to carry over the 1 so a second digit and you will get the number 11. Bases typically relate to a particular unit of measurement, for decimal it is the 10 fingers on both hands. As for Base-2, or Binary, it is based on the fact that computers are basically a large complex relay of switches that have 2 values, off or on. Off being 0 and on being 1, once you think about it in that respect it starts making sense.

Now to throw a curve ball in the mix lets talk about Base-16 which is called Hexadecimal. This has last digit values that reach but dont surpass 15. Now 15 is already 2 digits so taking our above examples it would look like this counts up

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15...time to carry over... 1:01?

that doesn't look very good because the double digit numbers and the carried values can be confused. So mathmaticians came up with another way to represent numbers 10-15 using the alphabet.

10 = A
11 = B
12 = C
13 = D
14 = E
15 = F

that means the count 1-16 looks like this:

1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10 (this may be confusing but in hexidecimal the number 10 = the value 16)

Dealing with binary (Base-2)

Normal counting is in decimal (Base-10) meaning a digit can hold 10 numbers 0-9 where as computers use binary, or Base-2, where digits can hold 2 numbers 0-1. So counting in would look like this:

0 = 000

1 = 001

2 = 010

3 = 011

4 = 100

5 = 101

If we wanted to find out what 10 looks like in binary we do the math out like this:

1   0   1   0

8 + 0 + 2 + 0 = 10

So the value for 10 in binary is 1010 = ( 8x1 + 2x1 ) = 10

The Other bases (Base-8 and Base-16)

Base-8 also known as octal and Base-16 also known as hexadecimal.

Octal

Hexadecimal

Bit Shifting

bits

In computing and telecommunications, a unit of information is the capacity of some standard data storage system or communication channel, used to measure the capacities of other systems and channels. In information theory, units of information are also used to measure the entropy of random variables and information contained in messages.

The most commonly used units of data storage capacity are the bit, the capacity of a system that has only two states, and the byte (or octet), which is equivalent to eight bits.

byte

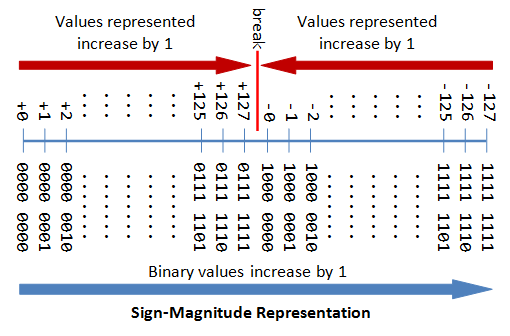
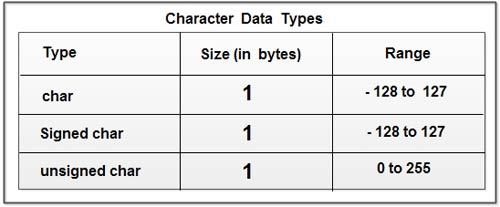
Historically, a byte was the number of bits used to encode a character of text in the computer, which depended on computer hardware architecture; but today it almost always means 8 bits – that is, an octet. A byte can represent 256 (28) distinct values, such as the integers 0 to 255, or −128 to 127.

word

Computers usually manipulate bits in groups of a fixed size, conventionally called words. The number of bits in a word is usually defined by the size of the registers in the computer's CPU, or by the number of data bits that are fetched from its main memory in a single operation. In the IA-32 architecture more commonly known as x86-32, a word is 16 bits.

dword

DWord stands for double word which as you guess is the same as a word but 32 bits instead on x86-32.

Primitive Data Structures

Data types are used within type systems, which offer various ways of defining, implementing and using them. Different type systems ensure varying degrees of type safety.

A computer’s way of saying this is what I expect this to be.

Integers

Represents a finite subset of mathematical numbers (0, 1, 2, …..) Comes in many flavors short / long signed/unsigned Example: (hex) FF would represent 255 (binary) 11111111 would represent 255

Boolean

This is a data type that denotes: (True/False), (On/Off) , (0,1)

1 = True and 0 = False

The Boolean data type is primarily associated with conditional statements, which allow different actions and change control flow depending on whether a programmer-specified Boolean condition evaluates to true or false.

Characters

A character is a unit of information that roughly corresponds to a character in the alphabet or symbol in a text language.

Characters can be represented in many ways but the usual methods are Unicode (UTF-8, UTF-16) and ASCII.

All of which use different sizes and map numbers to different characters.

Unicode (UTF-8 and UTF-16)

Shifting from UTF-8 -> UTF-16

UTF-8 = 1 byte while UTF-16 = 2 Bytes

As you can see 01000001 (41) is a capital A in UTF-8 and in UTF-16

The reason for more bits is to handle more characters without having to add more encodings.

ASCII

Abbreviated from American Standard Code for Information Interchange, is a character encoding standard. ASCII codes represent text in computers, telecommunications equipment, and other devices. Most modern character-encoding schemes are based on ASCII, although they support many additional characters. And it Supports the least Chars.

Floating Point Numbers

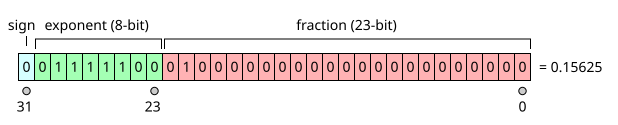
Floating-point arithmetic is arithmetic using formulaic representation of real numbers as an approximation so as to support a trade-off between range and precision.

Alphanumeric Strings

A string is traditionally a sequence of characters, is often implemented as an array data structure of bytes (or words) that stores a sequence of elements, typically characters, using some character encoding (hint: unicode and ascii).

Usually are null-terminated meaning the end of the string is denoted by a special terminating character, null byte (NULL), which is 00000000 (all zeroed out byte).

Reference

A reference is a value that enables a program to indirectly access a particular location in the computer's memory or in some other storage device.

Usually starting at a base address like 0x00000000 and moving up by the size of the data unit.

In the above example the ‘E’ would be at 0x00000002 that is 2 byte away from the offset (each char is 2 bytes, so we could assume they might be using UTF-16).